เซต เป็นคำใหม่ที่เราจะรู้จักตอนเรียน ม.4 ซึ่งจริง ๆ แล้ว เซต ก็คือ การบอกลักษณะที่เป็นกลุ่มของอะไรสักอย่าง เช่น เซตของจำนวนเฉพาะ หมายถึง กลุ่มของจำนวนเฉพาะ ดังนั้น สิ่งที่อยู่ในเซตนี้จะต้องเป็นจำนวนเฉพาะเท่านั้น เช่น 3 อยู่ในเซตของจำนวนเฉพาะ แต่ 4 ไม่อยู่ในเซตของจำนวนเฉพาะ
ซึ่งการอยู่ในเซต เรียกว่า เป็นสมาชิก สัญลักษณ์ คือ ∈
และถ้าไม่อยู่ในเซต เรียกว่า ไม่เป็นสมาชิก สัญลักษณ์ คือ ∉
นอกจากนี้ เซต มีความพิเศษอีกหนึ่งอย่าง คือ เมื่อมีของสองชิ้นเหมือนกันทุกประการจะถือว่าของสองชิ้นนั้นเป็นชิ้นเดียวเท่านั้น เช่น ถึงแม้ว่าเราจะใส่เลข 3 ลงไปในเซตของจำนวนเฉพาะเป็นจำนวน 4 ตัว เราก็จะถือว่ามีเลขสามเป็นสมาชิกแค่ตัวเดียวเท่านั้น และ ในเซต เราไม่คำนึงถึงว่าอะไรจะมาก่อนหรือหลัง
ในการเขียนเซตนั้นเราจะใช้เครื่องหมาย {} แทนเซต และใส่สมาชิกที่ต้องการไว้ข้างใน โดยใช้เครื่องหมาย , คั้นระหว่างสมาชิก เช่น {1,2,3,} หมายถึง เซตของ 1,2 และ 3
การเขียนเซตในโรงเรียนจะแบ่งออกเป็นสองประเภท คือ
1. การเขียนเซตแบบแจกแจงสมาชิก
เป็นการเขียนแบบที่สามารถเห็นสมาชิกในเซตเป็นตัว ๆ ได้เลย และบอกได้ทันทีว่าอะไรอยู่ในเซตนั้นบ้าง เช่น {2,4,6,8}
2. การเขียนเซตแบบมีเงื่อนไข
การเขียนเซตแบบมีเงื่อนไข จะใช้สัญลักษณ์ {} แทนเซตเหมือนกัน แต่สิ่งที่ใส่ลงไปจะไม่ใช้สมาชิกรายตัว แต่เป็นเงื่อนไขของการเป็นสมาชิก เช่น
{x|x เป็นจำนวนนับที่น้อยกว่าเท่ากับ 5}
เครื่องหมาย | จะแทนคำว่า โดยที่ หรือ คำว่า เมื่อ และ x จะเป็นตัวแปรที่แทนสิ่งที่จะอยู่ในเซตนี้ ดังนั้นเซตนี้ อ่านว่า เซตของ xโดยที่ x เป็นจำนวนนับที่น้อยกว่าเท่ากับ 5 ซึ่งจะได้ว่าสมาชิกในเซตนี้คือ 1,2,3,4 และ 5
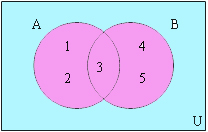
ในโรงเรียนจะแบ่งการเขียนเซตออกเป็น 2 ประเภทนี้เท่านั้น แต่พี่จะแนะนำการเขียนเซตอีกแบบ นั้นคือ การเขียนเซตแบบเป็นรูปภาพ ซึ่งปกติแล้ว ในโรงเรียนจะสอนเรื่องนี้อยู่ในหัวข้อ แผนภาพ เวนน์-ออยเลอร์ (Venn-Euler Diagram) ซึ่งการเขียนเซตด้วยภาพนั้น คือ การวาด รูปอะไรสักรูปที่เป็นรูปปิด ไม่ว่าจะเป็นวงกลม สี่เหลี่ยม สามเหลี่ยม หรือรูปอื่น ๆ ขอแค่เป็นรูปที่สามารถบอกได้ว่าส่วนไหนเรียกว่าข้างใน ส่วนไหนเรียกว่าข้างนอก แล้ว นำสมากชิกของเซตนั้นไปเขียนไว้ข้างในรูปนั้น เช่น {1,2,3,4,5} ถ้าต้องการเขียนเป็นภาพ จะได้
นอกจากนี้ เราจะมีการให้ชื่อเซต หรือ สัญลักษณ์แทนเซต เช่นถ้าเรามี {1,2,3,4,5} ถ้าเราต้องการพูดถึงเซตนี้บ่อย ๆ จะทำให้ยุ่งยากในการกล่าวถึง และสับสนได้ง่าย ดังนั้นเราจะให้ชื่อเซต โดยบอกว่า A={1,2,3,4,5} และหลังจากนี้เราจะเรียกแค่ เซต A เท่านั้น
ในการให้ชื่อเซตนั้น ควรเป็นตัวอักษรภาษาอังกฤษพิมพ์ใหญ่ เพื่อให้มีความเข้าใจที่ตรงกันและเป็นสากล
ในการหาจำนวนสมาชิกในแต่ละเซตก็คือ การหาว่าในเซตนั้นมีสิ่งที่อยู่ข้างในกี่ตัวเท่านั้นเอง เช่น
จำนวนสมาชิก ของ {2,4,6,8} คือ 4
จำนวนสมาชิกของเซต A ใช้สัญลักษณ์ n(A)
นอกจาการแบ่งเซตตามประเภทการเขียนเซตแล้ว ยังมีการแบ่งเซตตามจำนวนสมาชิกออกเป็น 2 ประเภท คือ
1. เซตจำกัด
เซตจำกัด คือ เซตที่สามารถนับจำนวนสมาชิกได้ ไม่ว่าจะนับออกมาเป็นจำนวนอะไรก็ตาม รวมถึง เซตที่มีจำนวนสมาชิกเป็น 0 ก็ถือว่าเป็นเซตจำกัดเหมือนกัน
เซตที่มีจำนวนสมาชิกเป็น 0 เรียกว่า เซตว่าง สัญลักษณ์คือ ∅
2. เซตอนันต์
เซตอนันต์ คือ เซตที่มีสมาชิกเยอะมากจนนับไม่ได้ หรือ บอกไม่ได้ว่าสมาชิกเป็นเท่าไหร่กันแน่ เช่น
{1,2,3,4,5,⋯}
เราจะไม่สามารถบอกได้ว่าสมาชิกมีเท่าไหร่กันแน่ ดังนั้น ถ้าเขียนเซตแบบแจกแจงสมากชิกแล้วมี ⋯ อยู่ที่หัวหรือท้ายเซต จะเป็นเซตอนันต์
แต่จะต้องระวัง ไม่ใช่ว่าเจอ ⋯ แล้วจะเป็นเซตอนันต์เสมอ เช่น {1,2,3,⋯,9,10} เซตนี้ มีจำนวนสมาชิกเท่ากับ 10 ดังนั้น เซตนี้จะต้องเป็นเซตจำกัด
เซตที่จะเท่ากัน คือ เซตที่เหมือนกันทุกอย่าง นั้นคือ มีจำนวนสมาชิกเท่ากัน และ สมาชิกทุกตัวเหมือนกัน
เช่น
{1,2,3,4,5} เท่ากับ {2,1,1,3,5,4}
เนื่องจากเราเคยบอกแล้วว่าในเซต ถ้ามีสมาชิกที่เหมือนกันทุกอย่างให้นับเป็นสมาชิกเพียงหนึ่งตัวเท่านั้น ดังนั้นทั้งสองเซตมีสมาชิกเท่ากัน คือ 5 และ ในเซตเราไม่คำนึงถึงว่า อะไรมาก่อนมาหลัง แต่ทั้งสองเซตประกอบด้วยเลข 1,2,3,4 และ 5 เหมือนกัน จึงได้ว่าเซตทั้งสองเซตนี้เท่ากัน
เวลาเราพูดสิ่งกลุ่มของอะไรสักอย่าง จะต้องมีการบอกขอบเขต เช่น เวลาพูดถึงกลุ่มของผู้หญิง ก็จะต้องดูว่าเรากำลังพูดกลุ่มของผู้หญิงจากกลุ่มใหญ่กลุ่มไหน เช่น กลุ่มของผู้หญิง จาก นักเรียนในห้องหนึ่ง จะได้ว่ากลุ่มที่่ใหญ่ที่สุดที่เป็นขอบเขตในการกล่าวถึงกลุ่มอื่น ๆ ในทีนี้คือนักเรียนทั้งหมดในห้องหนึ่ง
ดังนั้น ยูนิเวอส์ ก็คือ ขอบเขตในการกล่าวถึงกลุ่มต่าง ๆ หรือ เซตต่าง ๆ โดยสมาชิกในเซตต่าง ๆ ที่กล่าวถึงนั้นจะต้องอยู่ภายใต้ ยูนิเวอส์ นั้น ๆ
เมื่อ a,b,c เป็นจำนวนจริงใดๆ และ 
ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ a , b และ c และเมื่อค่าของ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ 
